ベイズの定理入門：初心者から学ぶ、簡単な解説と実践的な使い方

この記事では、数学と統計学の基本概念であるベイズの定理について、その理論的な背景から具体的な応用例まで、初心者にもわかりやすく解説します。条件付き確率の理解から、機械学習やAI技術におけるベイズの定理の使い方まで、簡潔かつ簡単な言葉で紹介します。数学が苦手な方や、統計検定、さらには機械学習の入門としてベイズの定理を学びたい方に最適な内容です。

第1章: ベイズの定理の基本

ベイズの定理とは

ベイズの定理は、条件付き確率に関する等式であり、ある事象Bが起こったもとで別の事象Aが起こる確率P(A|B)を、事象Aが起こったもとで事象Bが起こる確率P(B|A)を用いて求めるための定理です。具体的には、ベイズの定理は以下の式で表されます。

P(A|B) = {P(B|A) P(A)}/{P(B)}

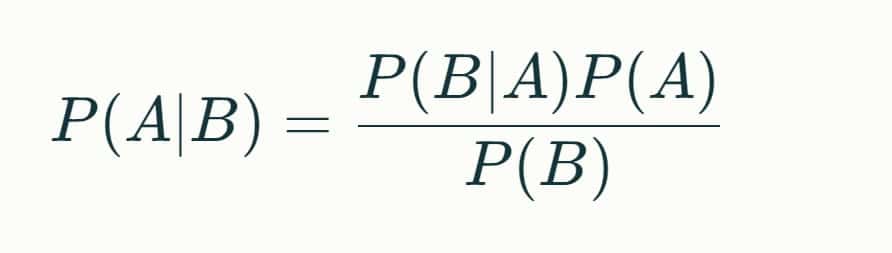
ここで、P(A|B)は事象Bが起こったもとで事象Aが起こる条件付き確率、P(B|A)は事象Aが起こったもとで事象Bが起こる条件付き確率、P(A)は事象Aが起こる確率（事前確率）、P(B)は事象Bが起こる確率です[1]。

ベイズの定理は、事後確率を求めるための定理として知られており、新しい情報が得られたときに、既存の事象の確率を更新することができます。この定理は、統計学、特にベイズ統計学の基礎となっており、医学、心理学、機械学習など多岐にわたる分野で応用されています[2][5][6]。

ベイズの定理の導出は、条件付き確率の定義式から始まります。条件付き確率の定義に基づき、事象AとBが同時に起こる確率P(A \cap B)を用いて、ベイズの定理の式を導き出します。この過程では、事象AとBの関係性を明確にし、新しい情報が与えられた状況下での事象の確率を再評価することが可能になります[2]。

ベイズの定理の重要性は、新しい情報を受け入れて事象の確率を更新する能力にあります。これにより、不確実性の中でより良い意思決定を行うための強力なツールとなっています[1][2][5][6]。

条件付き確率の基礎

条件付き確率は、ある事象が起こるという条件のもとで、別のある事象が起こる確率のことを指します。具体的には、事象Aが起こったときの事象Bが起こる確率を、条件付き確率と呼びます。この確率は、P(B|A)と表され、次の式により計算できます。

P(B|A) = {P(A∩B)}　/　{P(A)}

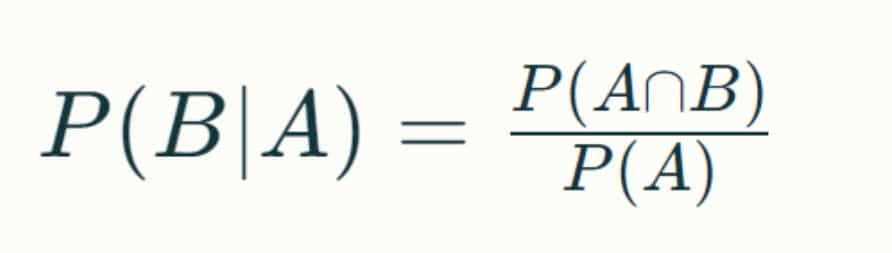
ここで、P(A ∩ B)は事象Aと事象Bが同時に起こる確率、P(A)は事象Aが起こる確率です。条件付き確率は、事象Aが起こったという情報が与えられた場合に、事象Bが起こる確率を再評価することを可能にします[3]。

例えば、ある袋の中に赤い玉と白い玉が入っているとします。赤い玉を取り出す事象をA、白い玉を取り出す事象をBとした場合、赤い玉を取り出した後に白い玉を取り出す確率は、条件付き確率を用いて計算することができます。

条件付き確率は、統計学や確率論において非常に重要な概念であり、実際のデータ分析や意思決定プロセスにおいても広く応用されています。例えば、医療分野では、ある病気の診断テストが陽性であった場合に、実際にその病気である確率を求めるのに条件付き確率が用いられます。また、マーケティング分野では、ある商品を購入した顧客が別の商品も購入する確率を求める際にも活用されます[3][6].

条件付き確率の理解は、確率論の基礎を学ぶ上で不可欠であり、より複雑な確率モデルや統計的推測の基礎となります。

第2章: ベイズの定理の導出

ベイズの定理の数学的導出

ベイズの定理の数学的導出は、条件付き確率と全確率の定理を基にしています。ベイズの定理は、ある事象Bが起こった後に、事象Aが起こる条件付き確率を計算するために使用されます。この導出過程では、事象AとBの関係を明確に理解することが重要です。

● 条件付き確率と全確率の定理

条件付き確率は、ある事象が起こったという条件のもとで、別の事象が起こる確率を表します。数学的には、事象Aが起こる確率をP(A)、事象Bが起こる確率をP(B)、事象AとBが同時に起こる確率をP(A∩B)とした場合、事象Bが起こった後に事象Aが起こる条件付き確率P(A|B)は次のように表されます。

P(A|B) = {P(A∩B)}/{P(B)}

全確率の定理は、複数の互いに排他的な事象が全体の事象空間を形成する場合に、ある事象の確率を計算するために使用されます。事象Bが起こる確率P(B)は、全ての互いに排他的な事象Eiに対して、次のように表されます。

P(B) = ∑_iP(B|E_i)P(E_i)

● ベイズの定理の導出

ベイズの定理の導出は、上記の条件付き確率と全確率の定理を組み合わせることで行われます。事象Aが起こった後に事象Bが起こる条件付き確率P(B|A)と、事象Aの確率P(A)、そして事象Bの確率P(B)を用いて、ベイズの定理は次のように表されます。

P(A|B) = {P(B|A)P(A)}/{P(B)}

ここで、P(B)は全確率の定理を用いて、複数の事象Eiに対して次のように計算されます。

P(B) = ∑_i P(B|E_i)P(E_i)

この式により、事象Bが起こった後に事象Aが起こる確率、つまり事象Aの事後確率を、事象Aの事前確率と事象Bの観測から更新することができます[1][3][5][6]。

ベイズの定理の導出は、事象間の関係を数学的に表現し、新たな情報が得られた際に確率を更新するための強力なツールを提供します。この定理は、統計学、機械学習、医療診断など、多岐にわたる分野で応用されています。

簡単な例で理解するベイズの定理

ベイズの定理は、ある条件が与えられたときに、特定の事象が起こる確率を計算するための方法です。この定理は、条件付き確率に関する等式であり、事象Aが起きたときに事象Bが起きる確率（P(B|A)）を、事象Bが起きたときに事象Aが起きる確率（P(A|B)）を用いて求めることができます。ベイズの定理の式は以下のように表されます。

P(A|B) = {P(B|A) × P(A)}/{P(B)}

ここで、P(A|B)は事象Bが起きたときに事象Aが起きる確率（事後確率）、P(B|A)は事象Aが起きたときに事象Bが起きる確率（尤度）、P(A)は事象Aが起きる確率（事前確率）、P(B)は事象Bが起きる確率（周辺確率）を表します。

● 具体例

簡単な例として、くじ引きの問題を考えてみましょう。6本のうち2本が当たりのくじがあるとします。Aさんが1本のくじを引き、当たりだったとします。このとき、Bさんが次にくじを引いたときに当たりを引く確率はどうなるでしょうか[1]。

この問題をベイズの定理で考えると、Aさんが当たりを引いた（事象A）後に、Bさんが当たりを引く（事象B）確率を求めることができます。事象Aが起きた後の事象Bの確率、つまりP(B|A)を求めることが目的です。

もう一つの例として、病気の検査があります。罹患率が0.01%の病気で、検査の判定が陽性だった場合、実際に病気である確率を求める問題です[3]。この場合、検査結果が陽性である（事象B）という条件のもとで、実際に病気である（事象A）確率、つまりP(A|B)をベイズの定理を用いて計算します。

これらの例から、ベイズの定理がどのようにして条件付き確率を計算するのか、そしてそれがどのように実際の問題解決に役立つのかが理解できます。ベイズの定理は、与えられた情報を基にして、事象の確率を更新する強力なツールです。

第3章: ベイズの定理の具体例と演習

具体的な応用例

ベイズの定理は、条件付き確率に関する等式であり、様々な分野で具体的な応用が見られます。以下に、ベイズの定理の応用例を紹介します。

● 1. 医療診断

ベイズの定理は、医療診断の精度を高めるために利用されます。例えば、ある病気の検査で陽性反応が出た場合、実際にその病気に罹患している確率を計算することができます。この計算には、病気の罹患率、検査の感度（病気の人が陽性と判定される確率）、特異度（病気でない人が陰性と判定される確率）が用いられます[3][7]。

● 2. スパムメールのフィルタリング

迷惑メールのフィルタリングにもベイズの定理が活用されています。メールの内容に特定の単語が含まれているかどうかなどの情報を基に、そのメールが迷惑メールである確率を計算します。この方法により、迷惑メールを効率的に識別し、フィルタリングすることが可能になります[6]。

● 3. 機械学習

機械学習、特にベイズ統計を用いた学習アルゴリズムでは、ベイズの定理が基礎となっています。データからモデルのパラメータを推定する際に、事前の知識（事前確率）と観測データを組み合わせて、より精度の高い推定（事後確率）を行います。このプロセスは、ベイズ更新とも呼ばれ、逐次的なデータの取得に対応することができます[5]。

● 4. 検索エンジンの予測変換

検索エンジンでは、ユーザーが入力したキーワードに基づいて、関連する検索候補を予測変換として表示します。この予測変換の精度を高めるために、ベイズの定理を用いたアルゴリズムが利用されることがあります。ユーザーの過去の検索履歴やクリック行動などのデータを基に、最も関連性の高い検索候補を提示することが可能になります[6]。

これらの例からもわかるように、ベイズの定理は多岐にわたる分野で具体的な応用が見られ、様々な問題解決に貢献しています。

実際の問題でベイズの定理を使ってみよう

実際の問題でベイズの定理を使ってみるために、具体的な例を挙げて解説します。ベイズの定理は、ある事象が起こった後に、それに関連する別の事象の確率を更新するために使用されます。以下の例を通じて、ベイズの定理の使い方を理解しましょう。

● 例題: 病気の診断テスト

ある病気が日本人の0.1%に発生しているとします。この病気を検出するテストがあり、病気に罹患している人がテストで陽性となる確率（感度）は99%、病気でない人がテストで陽性となる確率（偽陽性率）は3%です。ある人がこのテストを受けて陽性となった場合、その人が実際に病気に罹患している確率はどのくらいでしょうか。

● ベイズの定理の適用

ベイズの定理を適用するためには、以下の確率を定義します。

– P(A) : 病気に罹患している確率（事前確率）
– P(¬ A) : 病気に罹患していない確率
– P(B|A) : 病気に罹患している人がテストで陽性となる確率（感度）
– P(B|¬ A) : 病気でない人がテストで陽性となる確率（偽陽性率）
– P(A|B) : テストで陽性となった人が病気に罹患している確率（事後確率）

ベイズの定理により、事後確率 P(A|B) は以下のように計算できます。

P(A|B) = {P(B|A) · P(A)}/{P(B|A) · P(A) + P(B|¬ A) · P(¬ A)}

問題文から、以下の確率を得ます。

– P(A) = 0.001 （0.1%）
– P(¬ A) = 0.999 （100% – 0.1%）
– P(B|A) = 0.99 （99%）
– P(B|¬ A) = 0.03 （3%）

これらの値を上記の式に代入して計算すると、事後確率 P(A|B) が求められます。

P(A|B) = {0.99 · 0.001}/{0.99 · 0.001 + 0.03 · 0.999}

この計算を実行すると、テストで陽性となった人が実際に病気に罹患している確率が求められます。このようにベイズの定理を使って、テスト結果に基づいて病気の罹患確率を更新することができます[3][5]。

ベイズの定理は、医療診断のほかにも、迷惑メールのフィルタリング、機械学習における予測モデルの更新、法律における証拠の評価など、多くの分野で応用されています[1][2][4][6][7][8].

第4章: ベイズの定理と機械学習

機械学習でのベイズの定理の役割

機械学習におけるベイズの定理の役割は、不確実性の下での意思決定を可能にすること、および新しいデータが得られた際にモデルの予測を更新することにあります。ベイズの定理は、ある仮説（またはモデル）が与えられたときに、新しい証拠（データ）がその仮説の確率をどのように変化させるかを計算するために使用されます。これにより、機械学習モデルは、新しいデータに基づいてその予測を逐次的に改善することができます。

● ベイズの定理の基本

ベイズの定理は、事象A（仮説やモデル）と事象B（データ）の関係を表す数学的な式です。この定理は、事象Bが与えられたときの事象Aの条件付き確率、すなわち事後確率を、事象Aの事前確率、事象Bの周辺尤度、および事象Aが与えられたときの事象Bの条件付き確率（尤度）を用いて計算します[1]。

● 機械学習における応用

機械学習では、ベイズの定理を用いて、モデルのパラメータや予測に関する不確実性を定量化し、新しいデータが得られるたびにモデルを更新します。例えば、スパムフィルタリングでは、新しいメールがスパムである確率を計算するためにベイズの定理が使用されます。この確率は、メールの内容に基づいて逐次的に更新され、フィルタリングの精度を向上させます[1]。

● ベイズ推定と機械学習モデル

ベイズ推定は、ベイズの定理を基にした推定方法であり、機械学習モデルのパラメータを確率的に推定します。この方法では、パラメータの事前分布を設定し、新しいデータが得られるたびに事後分布を更新することで、モデルの不確実性を考慮した予測を行います[3][4]。

● 結論

ベイズの定理は、機械学習において重要な役割を果たします。この定理を用いることで、モデルは新しいデータに基づいてその予測を逐次的に更新し、不確実性の下での意思決定を可能にします。ベイズ推定を含むベイズの定理に基づく手法は、機械学習モデルの精度と信頼性を向上させるために広く利用されています。

ベイズ推定とベイズ統計学の基礎

ベイズ推定とベイズ統計学は、統計学の一分野であり、不確実性の下での推論や決定を行うための強力なフレームワークを提供します。この分野は、18世紀の数学者トーマス・ベイズにちなんで名付けられました。ベイズ統計学の核心は、ベイズの定理を用いて、事前の信念（事前確率）と新たに得られたデータを組み合わせて、事後確率を更新することにあります。このセクションでは、ベイズ推定とベイズ統計学の基礎について解説します。

● ベイズの定理

ベイズの定理は、条件付き確率と事前確率を用いて、ある仮説の事後確率を計算するための数学的な式です。式は以下のように表されます。

P(H|D) = {P(D|H) × P(H)}/{P(D)}

ここで、
– P(H|D) はデータ D が与えられたときの仮説 H の事後確率です。
– P(D|H) は仮説 H が真であるときにデータ D を観測する確率、すなわち尤度です。
– P(H) は仮説 H の事前確率です。
– P(D) はデータ D を観測する確率です。

● 事前確率と事後確率

ベイズ統計学では、事前確率と事後確率の概念が重要です。事前確率は、新たな証拠やデータを考慮する前に、仮説が真であると信じられる確率です。一方、事後確率は、新たな証拠やデータを考慮した後の、仮説が真である確率です。ベイズの定理を用いることで、事前確率から事後確率へと確率を更新することができます。

● ベイズ推定の応用

ベイズ推定は、さまざまな分野で応用されています。例えば、迷惑メールのフィルタリング、医療診断、機械学習、天文学、環境科学など、不確実性の下での意思決定が必要な場面で広く利用されています[3][6][17]。ベイズ統計学は、データから複雑なモデルを推定し、未知のパラメータに対する確率的な推論を行うことを可能にします。

● まとめ

ベイズ推定とベイズ統計学は、事前の知識や信念と新たに得られたデータを統合して、仮説やモデルの事後確率を更新する方法論です。ベイズの定理を用いることで、不確実性の下での推論や決定を行う際に、より情報に基づいたアプローチを取ることができます。この柔軟性と強力なフレームワークにより、ベイズ統計学は多岐にわたる分野での応用が期待されています。

第5章: ベイズの定理のさらなる応用

統計検定でのベイズの定理

統計検定では、ベイズの定理は重要な概念の一つです。ベイズの定理は、ある条件のもとでの事象の確率を求めるために用いられます。具体的には、ある結果が観測されたとき、それが特定の原因によるものである確率を計算するのに使用されます。この定理は、統計学における推論や意思決定のプロセスにおいて、事前に持っていた信念（事前確率）を新たに得られた証拠に基づいて更新する（事後確率に更新する）方法を提供します。

● ベイズの定理の基本形

ベイズの定理は以下の式で表されます。

P(A|B) = {P(B|A)・P(A)}/{P(B)}

ここで、
– P(A|B) は事象Bが起こった条件のもとで事象Aが起こる条件付き確率（事後確率）を表します。
– P(B|A) は事象Aが起こった条件のもとで事象Bが起こる条件付き確率を表します。
– P(A) は事象Aが起こる事前確率を表します。
– P(B) は事象Bが起こる確率を表します。

● 統計検定での応用例

統計検定では、ベイズの定理を用いた問題が出題されることがあります。例えば、特定の条件下での事象の確率を求める問題や、ある結果が得られたときにそれが特定の原因によるものである確率を求める問題などです。

1. 条件付き確率の計算：
– 条件付き確率の考え方と求め方を理解し、ベイズの定理を適用することで、ある事象が起こったという条件のもとで別の事象が起こる確率を計算します[3]。

2. 事後確率の更新：
– 新たな情報が得られたときに、事前確率を更新して事後確率を求める問題。例えば、製品が不良品であるという情報が得られたときに、その製品が特定の製造ラインから来た確率を更新する問題があります[1]。

3. 推定と意思決定：
– ベイズの定理を用いて、観測データから特定のパラメータや原因の推定を行い、それに基づいて意思決定を行う問題。これには、特定の条件下での最も可能性の高い原因を特定する問題などが含まれます[2]。

ベイズの定理は、統計検定だけでなく、統計学全般においても非常に重要な概念です。統計検定の受験者は、ベイズの定理の基本的な理解と、それを応用した問題解決能力を身につけることが求められます。

ベイズの定理を用いた先進的な研究事例

ベイズの定理は、条件付き確率を計算するための数学的な公式であり、統計学や確率論だけでなく、医学、ファイナンス、機械学習など多岐にわたる分野で応用されています。以下に、ベイズの定理を用いた先進的な研究事例を紹介します。

1. 医療診断の精度向上:
– 医療分野では、ベイズの定理を用いて、検査結果の正確性を向上させる研究が進められています。例えば、乳がんのスクリーニングにおいて、マンモグラフィの結果と患者の背景情報を組み合わせることで、乳がんの有無をより正確に判断することが可能になります[7]。

2. スパムメールのフィルタリング:
– ベイズの定理は、スパムメールのフィルタリングにも応用されています。メールの内容からスパムである確率を計算し、一定の閾値を超えたメールをスパムとして分類することで、ユーザーの受信箱を保護しています[8]。

3. 金融リスクのモデリング:
– 金融分野では、ベイズの定理を用いて、投資の成功確率や貸し倒れリスクを予測する研究が行われています。公開されている企業情報や過去のパフォーマンスを基に、将来の株価の動きやデフォルトの確率を計算することができます[2]。

4. 機械学習における予測モデルの改善:
– 機械学習では、ベイズの定理を用いて、モデルの予測精度を向上させる研究が進められています。特に、ベイズ推論を用いることで、不確実性を考慮した予測が可能になり、より信頼性の高いモデル構築が可能になります[3]。

5. 環境モニタリングにおける異常検出:
– 環境モニタリングにおいても、ベイズの定理は重要な役割を果たしています。センサーデータから異常な環境変化を検出し、早期に警告を発することで、自然災害のリスクを低減することが期待されています。

これらの事例からもわかるように、ベイズの定理はその柔軟性と汎用性により、多様な分野での研究や応用に貢献しています。今後も、ベイズの定理を基にした新たな技術や手法の開発が進むことが期待されます。

医学用語目次に戻る

プロフィール

この記事の筆者：仲田洋美（医師）

ミネルバクリニック院長・仲田洋美は、日本内科学会内科専門医、日本臨床腫瘍学会がん薬物療法専門医 、日本人類遺伝学会臨床遺伝専門医として従事し、患者様の心に寄り添った診療を心がけています。

仲田洋美のプロフィールはこちら